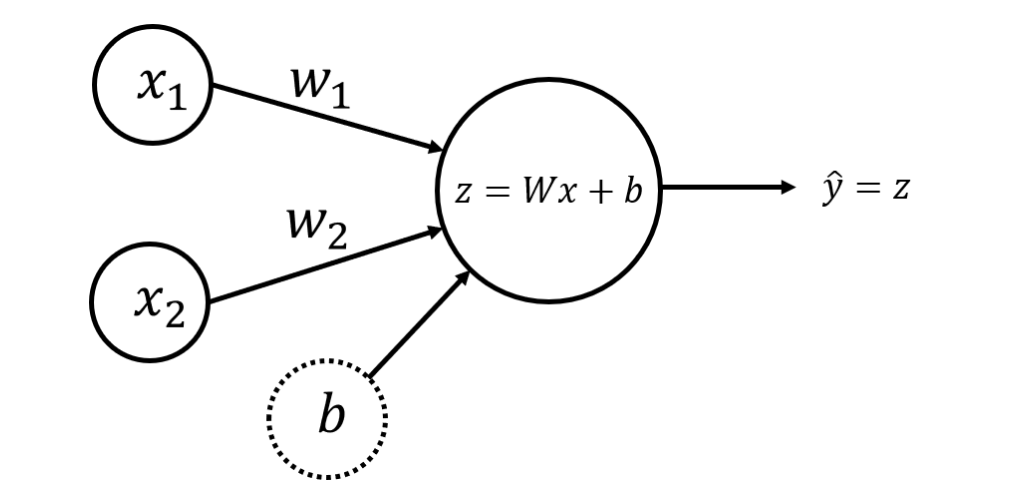
Neural Network for Regression

### Define Neural Network Functions
def layer_sizes(X, Y):
    n_x = X.shape[0]
    n_y = Y.shape[0]    
    return (n_x, n_y)

### Initiate Regresion Model Parameters
def initialize_parameters(n_x, n_y):
    W = np.random.randn(n_y, n_x) * 0.01
    b = np.zeros((n_y, 1))
    parameters = {"W": W,"b": b}
    return parameters

### Forward Propagation to generate Prediction
def forward_propagation(X, parameters):
    W = parameters["W"]
    b = parameters["b"]
    Z = np.matmul(W, X) + b             # Forward Propagation to calculate Z without the Activation Function
    Y_hat = Z
    return Y_hat

### Calculate Error from Prediction as Sum of Square Error
def compute_cost(Y_hat, Y):
    m = Y_hat.shape[1] 			        # Number of examples.
    cost = np.sum((Y_hat - Y)**2)/(2*m) # Compute the cost function.
    return cost

### Backward Propagation to find the Partial Derivative of Weights and Bias

def backward_propagation(Y_hat, X, Y):
    m = X.shape[1]

    # Backward propagation: calculate partial derivatives denoted as dW, db for simplicity. 
    dZ = Y_hat - Y
    dW = 1/m * np.dot(dZ, X.T)
    db = 1/m * np.sum(dZ, axis = 1, keepdims = True)
    grads = {"dW": dW,"db": db}
    return grads

### Update Parameters Using Gradient Descent of Learning Rate, the Derivative of Weights and Bias
def update_parameters(parameters, grads, learning_rate=1.2):
    W = parameters["W"] # Retrieve each parameter from the dictionary "parameters".
    b = parameters["b"]
    
    dW = grads["dW"] # Retrieve each gradient from the dictionary "grads".
    db = grads["db"]

    W = W - learning_rate * dW # Update rule for each parameter.
    b = b - learning_rate * db
    
    parameters = {"W": W,"b": b}
    return parameters

## Full Regression Model 
def nn_model(X, Y, num_iterations=10, learning_rate=1.2, print_cost=False):
    n_x = layer_sizes(X, Y)[0]
    n_y = layer_sizes(X, Y)[1]
    parameters = initialize_parameters(n_x, n_y)
    
    # Loop
    for i in range(0, num_iterations):
         
        # Forward propagation. Inputs: "X, parameters". Outputs: "Y_hat".
        Y_hat = forward_propagation(X, parameters)
        
        # Cost function. Inputs: "Y_hat, Y". Outputs: "cost".
        cost = compute_cost(Y_hat, Y)
        
        # Backpropagation. Inputs: "Y_hat, X, Y". Outputs: "grads".
        grads = backward_propagation(Y_hat, X, Y)
    
        # Gradient descent parameter update. Inputs: "parameters, grads, learning_rate". Outputs: "parameters".
        parameters = update_parameters(parameters, grads, learning_rate)
        
        # Print the cost every iteration.
        if print_cost:
            print ("Cost after iteration %i: %f" %(i, cost))

    return parameters

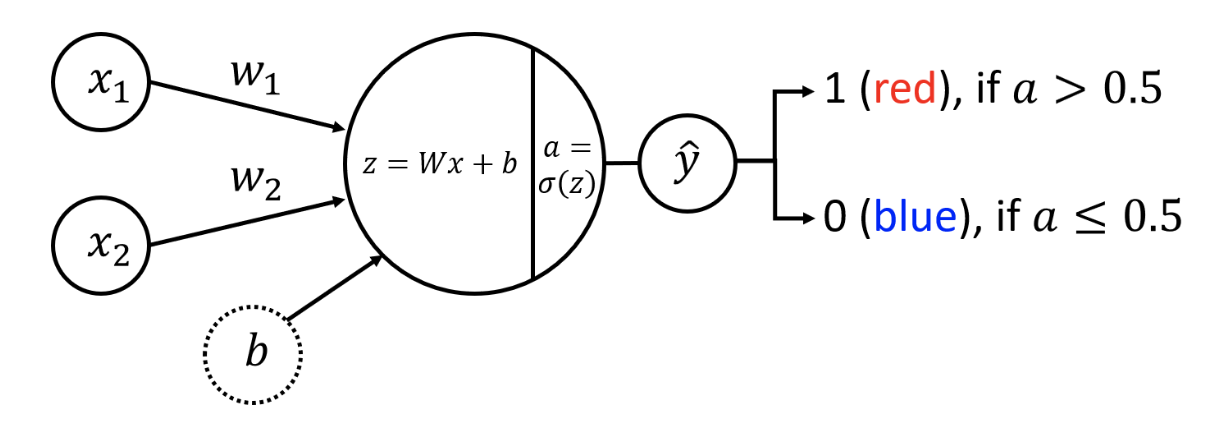
Neural Network for Classification

### Define Neural Network Function
def layer_sizes(X, Y):
    n_x = X.shape[0] ## Number of X features
    n_y = Y.shape[0] ## Number of Y features
    return (n_x, n_y)
    
### Initiate Model Parameters
def initialize_parameters(n_x, n_y):
    W = np.random.randn(n_y, n_x) * 0.01 ## Initialize Random value for Weights of each features
    b = np.zeros((n_y, 1))

    parameters = {"W": W, "b": b}
    return parameters

### Forward Propagation to generate Prediction
def forward_propagation(X, parameters):
    W = parameters['W']
    b = parameters['b']
    p = W@X + b
    activation = sigmoid(p)
    return activation

### Calculate Error from Prediction as Log Loss
def compute_cost(A, Y):
    m = Y.shape[1]
    ## Compute Log Loss 
    logprobs = - np.multiply(np.log(A),Y) - np.multiply(np.log(1 - A),1 - Y)
    cost = 1/m * np.sum(logprobs)
    return cost

### Backward Propagation find Derivative Gradients of Weight and Bias
def backward_propagation(A, X, Y):
    m = X.shape[1]
    dZ = A - Y
    dW = 1/m * np.dot(dZ, X.T)
    db = 1/m * np.sum(dZ, axis=1, keepdims=True)
    gradients = {"dW": dW, "db": db}
    return gradients 
    
### Fuction to Update Paramaters via Gradient Each Iteration
def update_parameters(parameters, grads, learning_rate=1.2):
    W = parameters["W"]
    b = parameters["b"]

    dW = grads["dW"]
    db = grads["db"]
    # print("Derivative", dW, db)
    
    W = W - learning_rate * dW
    b = b - learning_rate * db
    parameters = {"W": W, "b": b}
    
    # print("New Params ", W, b)
    return parameters
    
### Full Model Integration
def nn_model(X, Y, num_iterations=10, learning_rate=1.2, print_cost=False):
    n_x = layer_sizes(X, Y)[0]
    n_y = layer_sizes(X, Y)[1]

    params = initialize_parameters(n_x, n_y) ## Seed Starting Param Values


    # print("Starting Params", params)
    # LOOP with updating Params using Learning rate alpha
    for i in range(0, num_iterations):
        activations = forward_propagation(X, params)
        cost = compute_cost(activations, Y)
        gradients = backward_propagation(activations, X, Y)
        params = update_parameters(
            params, 
            gradients, 
            learning_rate
        )
        # print("New Params", params)
        if print_cost:
            print("Cost after iteration %i: %f" %(i, cost))
            
    return params