Ultilize Monte Carlos Method to Explore All Black Jack Game State and Train Our Agent via 500000 game to find optimal strategy

# ============================================================
# blackjack_training.py
# Monte Carlo Control for Blackjack (Gymnasium)
# ============================================================

import gymnasium as gym
import numpy as np
from collections import defaultdict
import pickle
import matplotlib.pyplot as plt

# --- Training Parameters ---
EPISODES = 500_000
GAMMA = 1.0
EPSILON = 0.1

# --- Environment ---
env = gym.make("Blackjack-v1", sab=True)

# --- Q-value table ---
Q = defaultdict(lambda: np.zeros(env.action_space.n))
returns_sum = defaultdict(float)
returns_count = defaultdict(float)

# --- Epsilon-greedy policy ---
def epsilon_greedy_policy(state, Q, epsilon=0.1):
    if np.random.random() < epsilon:
        return env.action_space.sample()
    return np.argmax(Q[state])

# --- Monte Carlo Control (First-Visit) ---
for ep in range(EPISODES):
    episode = []
    state, _ = env.reset()
    done = False

    while not done:
        action = epsilon_greedy_policy(state, Q, EPSILON)
        next_state, reward, done, truncated, _ = env.step(action)
        episode.append((state, action, reward))
        state = next_state

    # Backward returns update
    G = 0
    visited = set()
    for t in reversed(range(len(episode))):
        s, a, r = episode[t]
        G = GAMMA * G + r
        if (s, a) not in visited:
            visited.add((s, a))
            returns_sum[(s, a)] += G
            returns_count[(s, a)] += 1
            Q[s][a] = returns_sum[(s, a)] / returns_count[(s, a)]

    if (ep + 1) % 100000 == 0:
        print(f"Episode {ep + 1}/{EPISODES} complete.")

# --- Save learned Q-table ---
with open("blackjack_Q.pkl", "wb") as f:
    pickle.dump(dict(Q), f)

print("✅ Training finished and Q-table saved as blackjack_Q.pkl")


# ============================================================
# Visualization of learned value function
# ============================================================

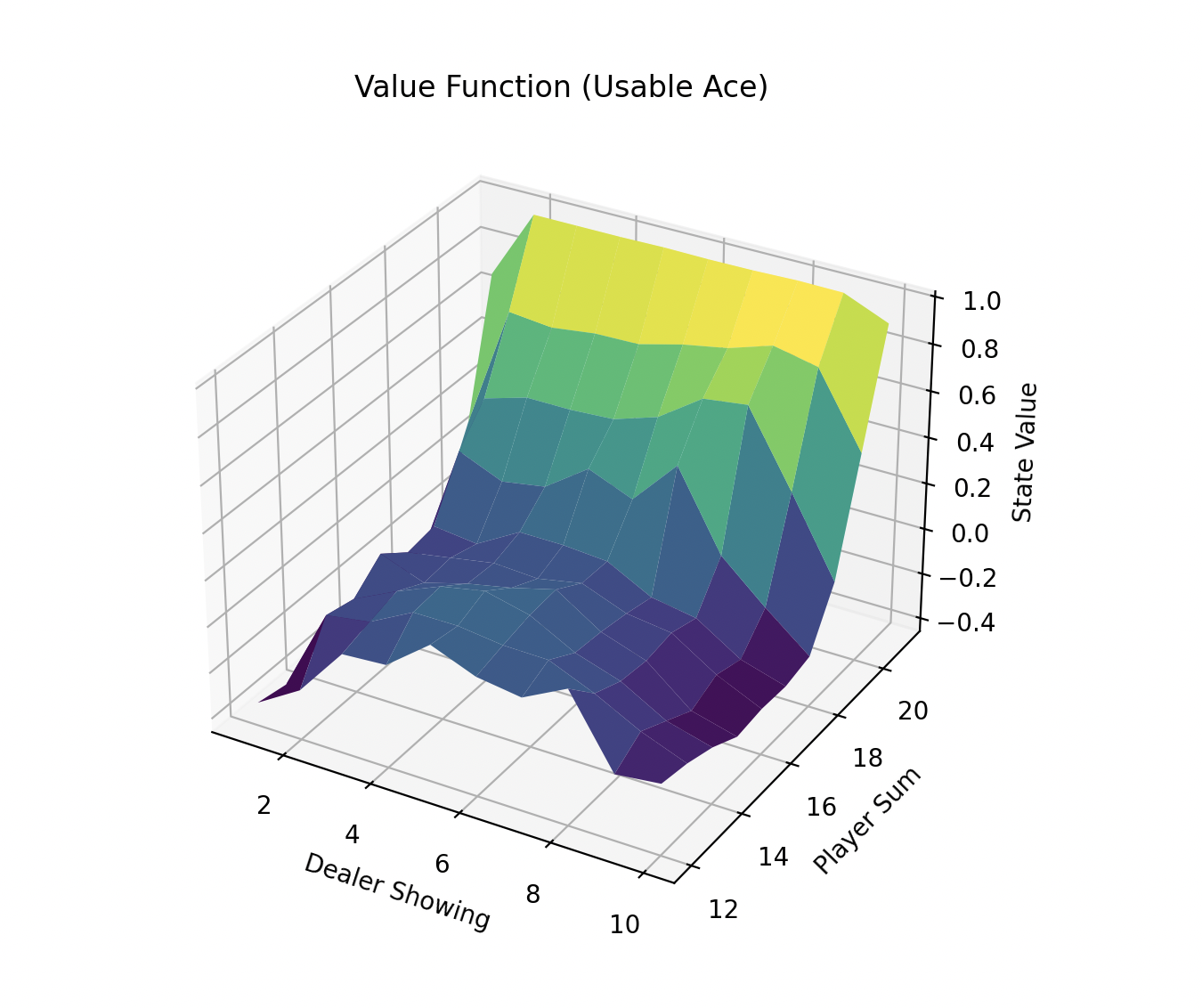
def plot_value(Q, usable_ace=True):
    """
    Plots the value function as a 3D surface.
    """
    player_sums = np.arange(12, 22)
    dealer_showing = np.arange(1, 11)
    values = np.zeros((len(player_sums), len(dealer_showing)))

    for i, ps in enumerate(player_sums):
        for j, ds in enumerate(dealer_showing):
            s = (ps, ds, usable_ace)
            if s in Q:
                values[i, j] = np.max(Q[s])  # best action value
            else:
                values[i, j] = 0.0

    fig = plt.figure(figsize=(9, 6))
    ax = fig.add_subplot(111, projection="3d")
    X, Y = np.meshgrid(dealer_showing, player_sums)
    ax.plot_surface(X, Y, values, cmap="viridis")
    ax.set_xlabel("Dealer Showing")
    ax.set_ylabel("Player Sum")
    ax.set_zlabel("State Value")
    title = "Usable Ace" if usable_ace else "No Usable Ace"
    ax.set_title(f"Value Function ({title})")
    plt.show()


# --- Plot both value surfaces ---
plot_value(Q, usable_ace=True)
plot_value(Q, usable_ace=False)

print("📊 Plots generated successfully!")

Simulate Black Jack Game Play in Gymnasium Enviroment with Python

# ============================================================
# blackjack_play.py
# Visual Blackjack Simulation using learned Q-table
# ============================================================

import gymnasium as gym
import numpy as np
import pickle
import time
from collections import defaultdict

# --- Load Q-table ---
with open("blackjack_Q.pkl", "rb") as f:
    Q_dict = pickle.load(f)

Q = defaultdict(lambda: np.zeros(2), Q_dict)
policy = {s: np.argmax(Q[s]) for s in Q}

# --- Create environment with render mode ---
env = gym.make("Blackjack-v1", render_mode="human", sab=True)

def play_visual(policy, n_episodes=5, delay=1.0):
    for ep in range(n_episodes):
        state, _ = env.reset()
        done = False
        total_reward = 0
        print(f"\n=== Episode {ep + 1} ===")
        time.sleep(delay)

        while not done:
            action = policy.get(state, env.action_space.sample())
            next_state, reward, done, truncated, _ = env.step(action)
            total_reward += reward
            state = next_state
            time.sleep(delay)

        print(f"Final reward: {total_reward}")
        time.sleep(1.5)

    env.close()

# --- Run Visual Simulation ---
play_visual(policy, n_episodes=10, delay=0.8)