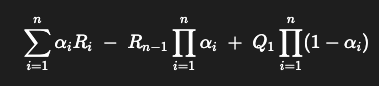The K-Armed Bandit Problem

The K-Armed bandit problem is an reinforcement learning usecase where our Bandit has the options of using K different types of Arm to conduct his robbery. A different weapon from the set of K different arms will yield different reward with a known probability distribution each time our Bandit conduct their robbery. Our program needs to help our bandit agents to conduct their n-numbers of bank robberies as optimal as possible to maximize their total rewards.

We applies our K-Armed Bandit strategy for our bandit by ultilizing the highest value weapon within their k-armed arsenal (1-Epsilon) percentage of time as their Greedy Moves but also mix in with Random Moves at Epsilon percentage of time to discover higher value weapons. We will then use our Learning from Random Move to update our Action Value for each weapons and select a new weapon as our Greedy Move for following roberries.

We will use the NUMPY Argmax module np.argmax() in our Python program to find the current Highest Value weapon for each of our iterations.

Python Program for the K-Armed Bandit Problem

In the python implementation above, we use the Incremental Implementation to save memory and computation requirement. Value of action is updated incrementally in each iteration after the reward is acquired

value = self.values[chosen_arm]
updated_value = ((c-1)/c) * value + (1/c) * reward 
self.values[chosen_arm] = updated_value

The Incrementation Implementation could be expressed in Formula or Python code

updated_value = ((c-1)/c) * value + (1/c) * reward 

K-Armbed Bandit Reinforcement Learning Exercises

Exercise 2.1: In e-greedy action selection, for the case of two actions and e = 0.5, what is the probability that the greedy action is selected?

With e = 0.5, we will select random action 50% of time while selecting greedy action 50% of time. There are only two actions option available so the probability of selecting greedy action is 0.5 and 0.25 from random action so total 0.75 or 75% of time.

Exercise 2.2: Bandit example Consider a k-armed bandit problem with k = 4 actions, denoted 1, 2, 3, and 4. Consider applying to this problem a bandit algorithm using e-greedy action selection, sample- average action-value estimates, and initial estimates of Q1(a) = 0, for all a. Suppose the initial sequence of actions and rewards is A1 = 1,R1 = 1,A2 = 2,R2 = 1,A3 = 2,R3 = 2,A4 = 2, R4 = 2, A5 = 3, R5 = 0. On some of these time steps the e case may have occurred, causing an action to be selected at random. On which time steps did this definitely occur? On which time steps could this possibly have occurred?

Step 5 with Action 3 selected and reward equal 0 definitely a Random action selection. While Step 1 could a known greedy action selection or a random action selection.

Exercise 2.3: In the comparison shown in Figure below, which method will perform best in the long run in terms of cumulative reward and probability of selecting the best action? How much better will it be? Express your answer quantitatively.

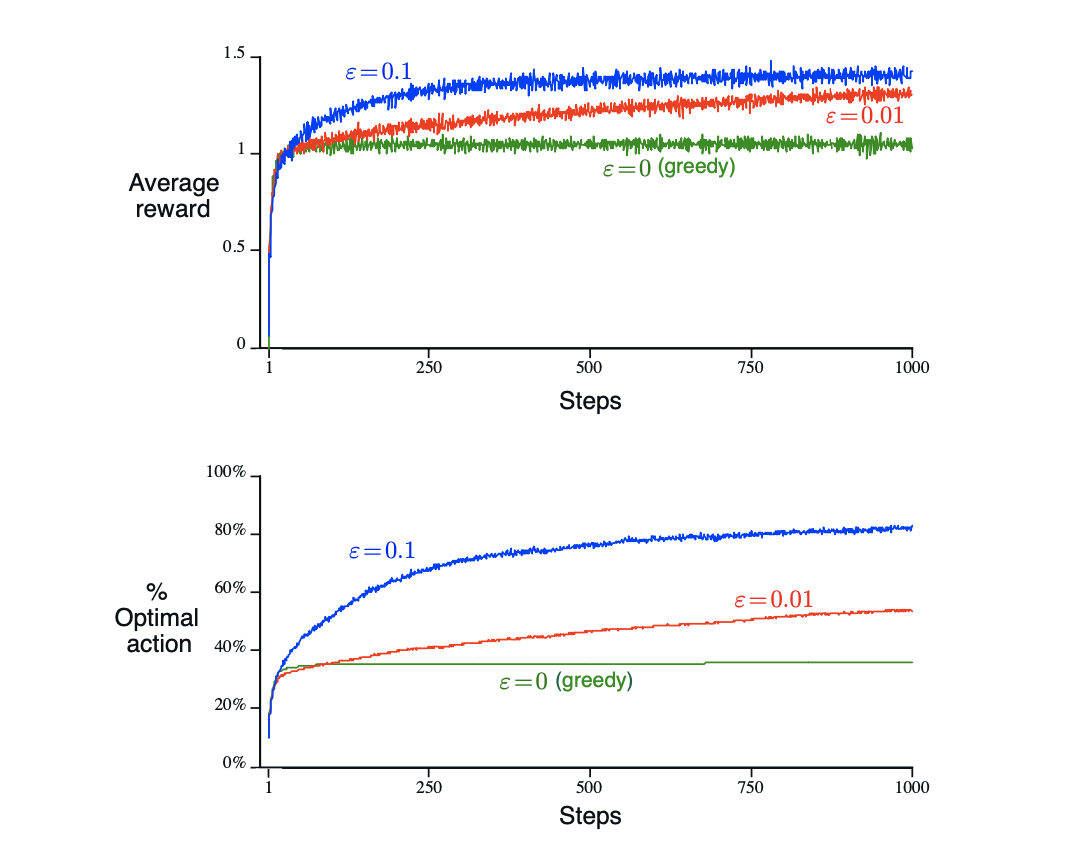
In the long run, the epsilon-greedy of 0.1 will perform the best. 10% of random action allows the algorithm to find its more optimal moves and perform 50% better than greedy action only and 20% better than 1% random action.

Exercise 2.4: If the step-size parameters, αn, are not constant, then the estimate Qn is a weighted average of previously received rewards with a weighting different from that given by (2.6). What is the weighting on each prior reward for the general case, analogous to (2.6), in terms of the sequence of step-size parameters?.

Formula to evaluate Current value as Weighted Average of the Past Reward and Starting Value

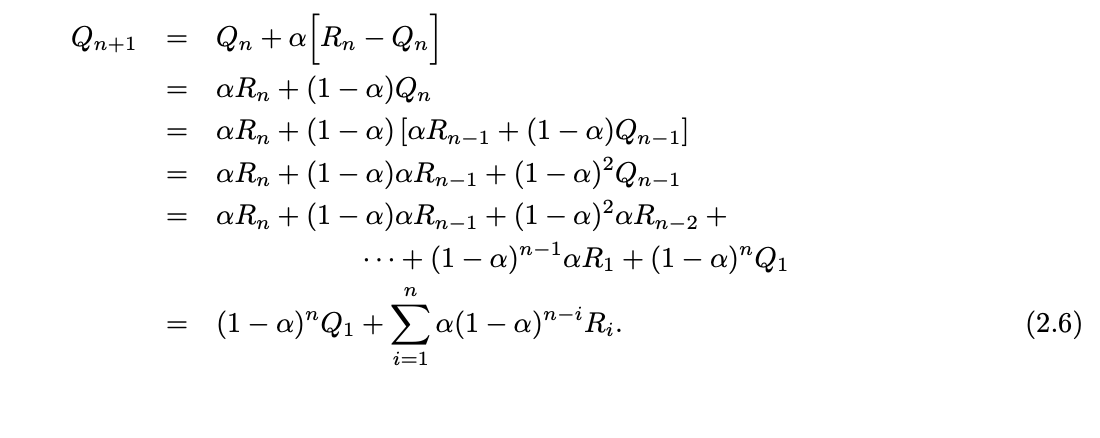
Formula to evaluate Current value in term of sequences of Changing Step-Size Parameter