What is Gradient Descent ?

Gradient Descent are methods to find the Minimum of a Function by calculating and approximating its Derivative toward the value of Zero. When the Derivative or the Slope of the Function is Zero, it is at its local or global minimum.

When we apply the Gradient Descent method on a Loss Function, it helps to find the Weights and Bias that miminizing this Loss Function or most accurately predict our expected outcome.

Gradient Descent on 1 Variable Function

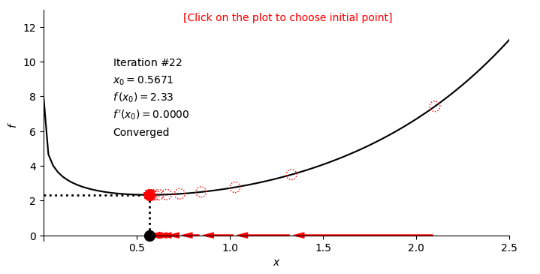
### Gradient Descent on e^(x) - log(x) to find the Slope 0 Minimum Point

def f_example_1(x):
    return np.exp(x) - np.log(x)

def dfdx_example_1(x):
    return np.exp(x) - 1/x

def gradient_descent(dfdx, x, learning_rate=0.1, num_iterations = 100):
    for iteration in range(num_iterations): ### Iterate 100 time
        print(iteration, x)
        x = x - learning_rate * dfdx(x)     ### Increment Down X value by learning_rate * derivative
    return x

initial_x = 1.0
gradient_descent(dfdx_example_1, initial_x, 0.1, 1000)

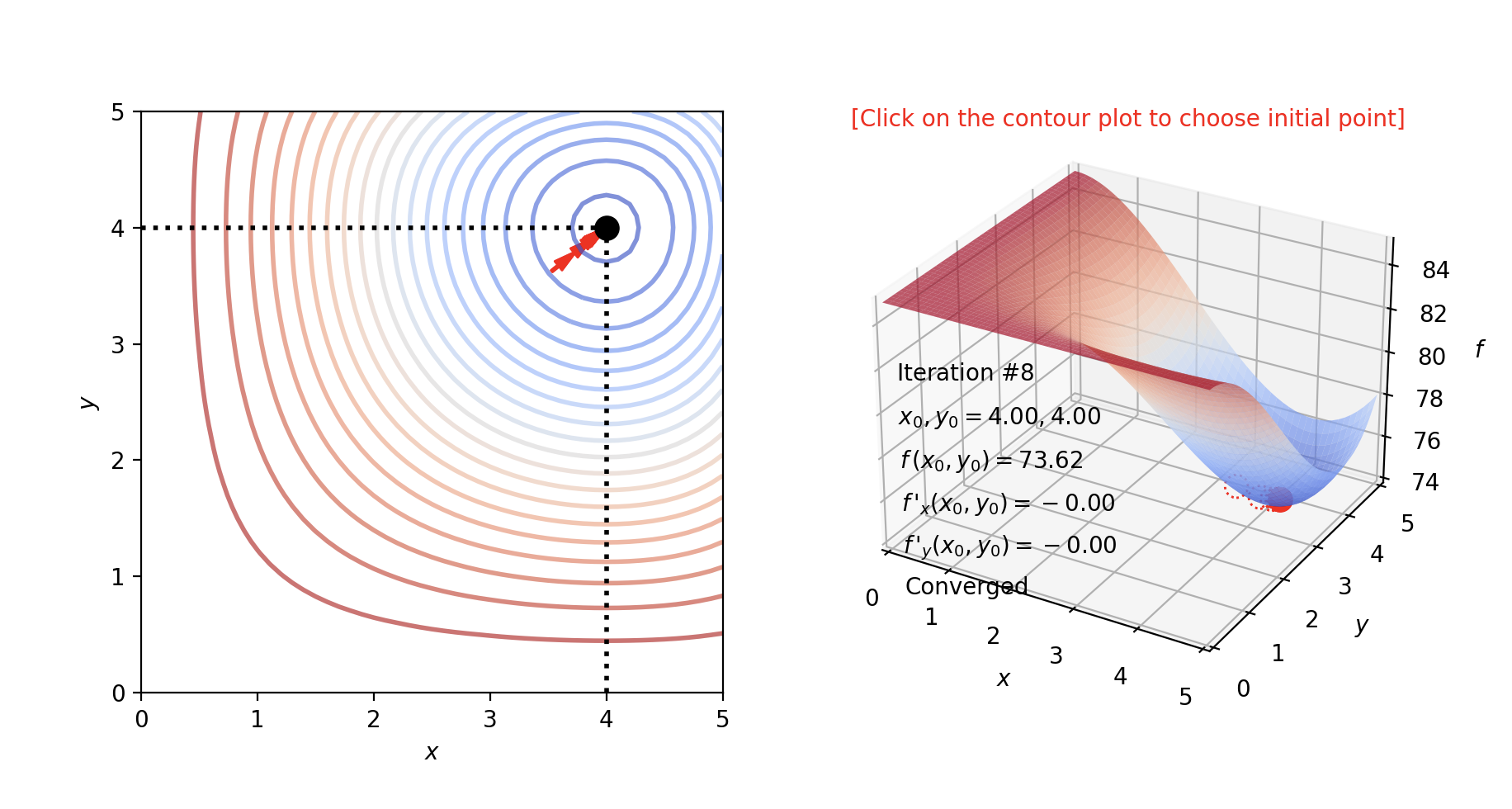
Gradient Descent on 2 Variables Function

### Gradient Descent on function (85+0.1(-1/9*(x-6)*x^2*y^3 + 2/3*(x-6)*x^2*y^2))
def f_example_3(x,y):
    return (85+ 0.1*(- 1/9*(x-6)*x**2*y**3 + 2/3*(x-6)*x**2*y**2))

def dfdx_example_3(x,y):
    return 0.1/3*x*y**2*(2-y/3)*(3*x-12)

def dfdy_example_3(x,y):
    return 0.1/3*(x-6)*x**2*y*(4-y)

def gradient_descent(dfdx, dfdy, x, y, learning_rate = 0.1, num_iterations = 100):
    for iteration in range(num_iterations):
        x, y = x - learning_rate * dfdx(x, y), y - learning_rate * dfdy(x, y)
    return x, y