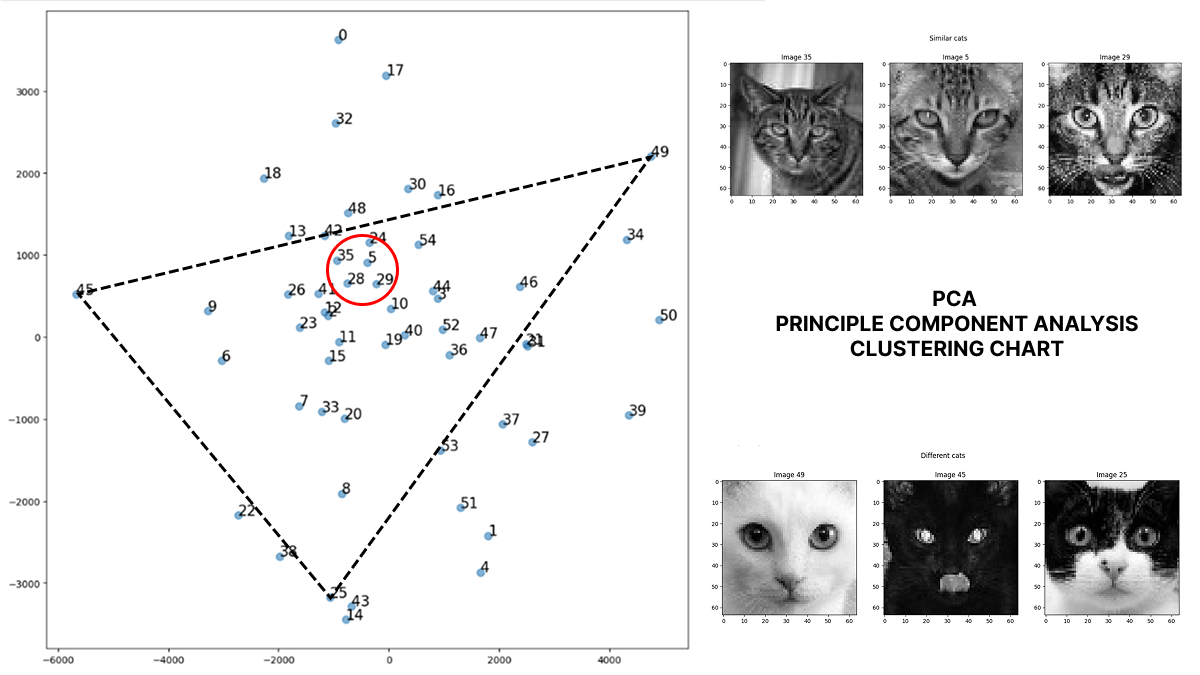
Principle Component Analysis PCA is a Machine Learning method to reduce the Dimension and Complexity of Data, Re-Balance the Dataset on the most Important Valuable features. With PCA, we can easily Cluster Our Data to find closely similiar and widely different data point.

PCA Principle Component Analysis for an Image dataset including 6 different steps:

• Flatten the 2D Image to Single Row Vector format
• Center the Data against its Mean Value
• Calculate the Covariance Matrix
• Calculate and Rank the Eigen-value and Eigen-matrix from the Covariance Matrix
• Perform PCA Dot Product between 2 or 3 highest value Eigen-Matrix Pricipe Components and the original Dataset
• Plot PCA result to find Dataset Clustering

import numpy as np
import scipy.sparse.linalg

###
### Flatten 2D Image to Single Row vector
###

imgs_flatten = np.array([im.reshape(-1) for im in imgs])

###
### Center the Data
###

def center_data(Y):
    mean_vector = np.mean(Y, axis=0)                          ### Find Mean Vector of Features for all 55 samples
    print("Mean Vector\n",mean_vector)
    mean_matrix = np.repeat(mean_vector, Y.shape[0])          ### Generate 1 single row 55x4096 Mean Matrix from Mean Vector
    # print("Matrix Shape ", mean_matrix.shape)
    mean_matrix = np.reshape(mean_matrix, Y.shape, order="F") ### Generate 55 rows 55x4096 Mean Matrix from Mean Vector
    X = Y - mean_matrix                                       ### Center All Datapoint by Removing Mean Matrix from Y
    return X

X = center_data(imgs_flatten)

###
### Calculate Covariance Matrix
###

def get_cov_matrix(X):
    ### Getting Covariance Matrix by Cal Dot Product of XT and X 
    ### and divide by number of observation -1 
    obs_n = X.shape[0]-1      
    cov_matrix = np.dot(X.T, X)/obs_n
    return cov_matrix

cov_matrix = get_cov_matrix(X)


###
### Calculate and Rank EIGEN-VALUE and EIGEN-VECTOR
###

eigenvals, eigenvecs = scipy.sparse.linalg.eigsh(cov_matrix, k=55)
eigenvals = eigenvals[::-1]       ### Invert the Order of Eigenvals
eigenvecs = eigenvecs[:,::-1]     ### Invert the Order of Eigenvecs

###
### Perform PCA for Most VALUABLE Princple Components of the Dataset
###

Xred2 = perform_PCA(X, eigenvecs,2)
def perform_PCA(X, eigenvecs, k):
    V = eigenvecs[:, :k] ## Select most valuable K component
    Xred = np.dot(X, V)  ## Perform Dot product on the Centered Data 
    return Xred

### By Plotting the PCA Result we find the high similar or widely different images